The Analytic Hierarchy Process (AHP) is a multi-criteria decision-making process based on mathematics and psychology. The mathematician Dr. Thomas L. Saaty developed this process in the 1970s. The AHP is a decision support tool, which has been widely used to solve complex decision problems. It has multi-level hierarchical structure of objectives, criteria and alternatives. It is a method for assessing and prioritizing options. The AHP guides practitioner to use a set of pairwise comparisons to derive the pertinent data. These comparisons are weighed and measured for each individual decision criterion
To summarize, the Analytical hierarchy process provides a logical framework to determine the benefits of each alternative. And it can be used for a wide variety of applications, such as:
- Strategic planning
- Resources allocation
- Product marketing
- Business selection
- Industrial engineering
- Government decision
Broad steps in Analytical Hierarchy Process
- State the objective
- Define the criteria’s and evaluate
- Pick the alternatives and evaluate
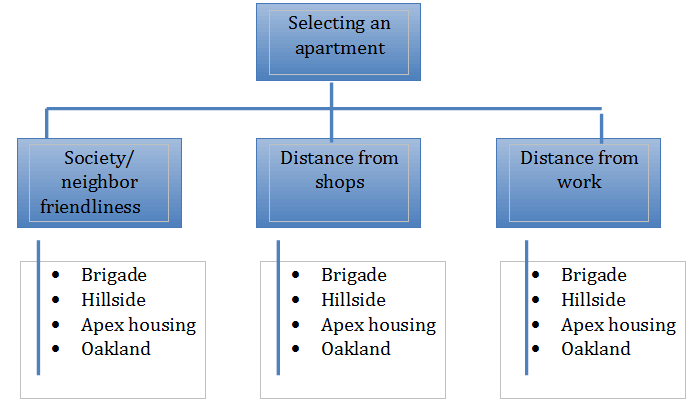
This information is then arranged in hierarchical tree. Let us understand this with an example, where objective is to select an apartment.
Pairwise comparison
One of the most crucial steps in many decision-making methods is the accurate estimation of the pertinent data. Using pairwise comparisons, the relative importance of one criterion over another can be expressed. Is option 1 more important than option 2? If yes, quantify by how much?
The AHP can adopt either of the following ways to analyze the objective
- Cross tabulation
- Rank Based Evaluation
- Weight Criteria
- Rank Reversal
Let us elaborate on cross tabulation for the given example. For selecting an apartment, we have 4 alternative choices Brigade, Hillside, Apex housing and Oakland and 3 criteria to decide the alternatives society/neighbor friendliness, distance to shops and distance to work. The range is set for each criterion, where higher values are preferable than small or negative values.
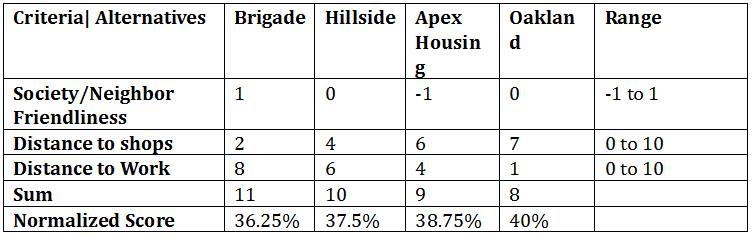
In this case higher normalized score corresponds to higher preference. Clearly the choice is Oakland apartment considering all the criteria.
However, cross tabulation technique has certain limitations. It is quite unfair to sum all the values of multiple criteria and compare the result. Certain factors clearly are dominant with higher ranges. To be fair, we can propose two solutions:
- Instead of using random values for each criterion, we can rank the alternatives for each criterion. Smaller rank value is more preferable than the higher rank.
- We transform the score value of each criterion according to the range value such that each criterion will have the same range
