ANOVA stands for ‘Analysis of Variance’. It actually means analysis of variation in means of different groups of a population or different populations. It is an advanced version of t – test. While t-test is used to compare two means, ANOVA can be used for more than two means.
What does an ANOVA do?
It studies whether the variation between group-means is due to an effect/treatment of it is just a chance variation. It checks the ‘Between Group Variation’ and ‘Within Group Variation’. If the treatment has a significant effect, then ‘Between Group Variation’ will be significantly higher than ‘Within Group Variation’.
How to do an ANOVA test?
Assume an educational institute wants to check whether different modes of education like: Visual aided teaching, practical learning, Self-learning through library & internet, have an impact on the students’ performance. The management decided to assign 20 students to each of the teaching methods. Their performance will be evaluated with an examination at the end of treatment. The scores are collected and the mean scores of each of the methods are also arrived.
ANOVA method is used to find out, if there is a difference between the mean values of the three groups.
Like in all other Hypothesis Testing, the hypothesis of ANOVA is like:
Null hypothesis: Mean of all the three methods are equal
Alternate Hypothesis: There is a significant variation in mean in at least one of the methods
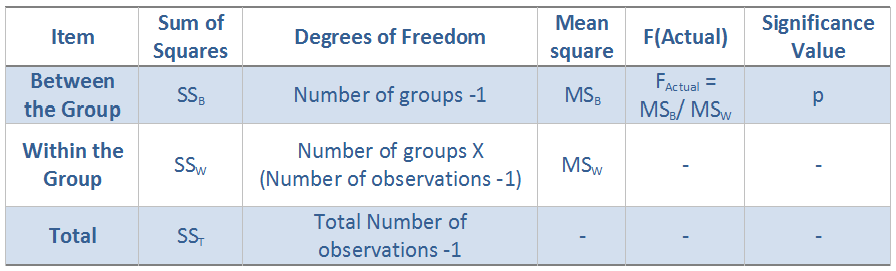
- Calculate the Sum of Squares of ‘Between the Group’ SSB.
- Calculate the Sum of Squares of ‘Within the Group’ SSW.
- Find the degrees of freedom of ‘Between the Group’: df1 = Number of groups -1
- Find the degrees of freedom of ‘Within the Group’: df2 = Number of groups X (Number of observations -1)
- Calculate the Mean Square value for ‘Between the Group’. MSB= SSB/ df1
- Calculate the Mean Square value for ‘Between the Group’. MSW = SSW/ df2
- Calculate F value. FActual = MSB/ MSW
- Find from F-Table, the FExpected value for the given degrees of freedom.
- Find out the significance value ‘p’ value.
The below table will explain how the calculations are performed and interpreted:
There are two ways to find out if the variation. If there is a significant difference between the mean values of groups, FActual will be greater than FExpected.
Another way is: p value will be less than α. Then null hypothesis cannot be validated. Thus alternate hypothesis is accepted.
Types of ANOVA
ANOVA has multiple uses and there are various types that can be used for different purposes:
- One-way ANOVA: Used to compare means of groups/populations using one factor.
- Two-way ANOVA: Used to compare means of groups/populations using two factors.
- Two-way ANOVA (Repeated): Used to compare means of groups/populations using two factors with interactions among the factors
- Nested ANOVA: Used to compare means of groups/populations that can be sub-grouped and the interactions happen only within the sub-groups and not with other factors.
Thus ANOVA can be used for various purposes. This article is just an introduction to ANOVA. Each type of ANOVA has some variations and the methods and interpretations will be different.