Introduction
Economic order quantity (EOQ) also known as Wilson Formula founded by Ford W. Harris in the year 1913 helps in determining the optimum level of inventory that needs to be ordered so that the total inventory cost is reduced. In any inventory model, whether continuous or fixed order quantity, whenever the inventory level reaches below a specific level also called as reorder point, fresh inventory is ordered again to fill the gap and raise the inventory level to meet the demand. This order itself would bear ordering cost and inventory carrying cost.
The two important categories of cost in inventory cost are ordering cost and carrying cost.
- Ordering costs: This costs is incurred while obtaining additional inventories. This include costs incurred while communicating the order and transportation.
- Carrying costs: This cost is incurred for holding the inventory. This include the opportunity cost, storage costs and spoilage cost.
We need to minimize the total inventory cost by reducing both ordering and carrying cost and EOQ model helps us in achieving it.
3
2+6
Total inventory costs = Ordering costs + Holding costs
Assumptions: But EOQ is applicable only when the demand for a product is constant. Ordering Cost is a fixed cost. There is cost for storage, also known as holding cost.
Inventory Cost Optimization
EOQ model helps in calculating the optimal order size that would minimize the inventory cost. The purpose is to order desired quantity at least cost.
- If the inventory order quantity is less, than it may incur more fixed ordering cost because whether 1 unit is ordered or more, the ordering cost remains the same. More is the quantity, lesser will be the ordering cost per unit.
- If the inventory order quantity is more, than it may incur more inventory carrying cost. More is the quantity more will be the carrying cost
Ordering cost and Carrying cost are anti-proportional to each other. If one of this cost decreases, it would lead to increase of other cost. So it is not possible to keep on decreasing both the cost at the same time. EOQ model defines a quantity which maintains the balance for both Ordering Cost and Carrying Cost and suggests an optimal quantity which is suitable to order in maintaining the minimum inventory cost for ordered quantity.
Example
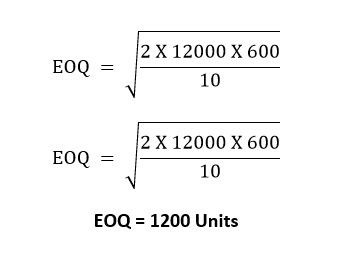
The annual demand for an item is 12000 Units. The unit cost of the item is Rs. 50. The inventory carry cost/unit/year is 20% of the unit cost. The ordering cost per order is Rs 600.
Annual Demand = 12000 Units
Ordering Cost per Order = Rs 600
Carry Cost per unit per year = 20% of Rs 50 = Rs 10
Conclusion
1200 Units is the optimal quantity that should be re-ordered so that the total inventory cost is minimum.

